虚数总是困扰着我们,就像自然底数e一样。有很多小概念看起来太过平常,不求甚解的人觉得这有什么,这都是数学家的事,或者会对着自己一脸好奇的孩子说“等你到大学的时候就懂了”,许多孩子童年的求知欲受挫可能都是来自于家长的这一句话看似安慰的话。所以,如果不主动去了解,不仅自己会错过很多醍醐灌顶的机会,还会阻碍下一代的思想进步。
在说虚数(Imaginary Numbers)之前,应该先提大家更加熟悉的一个概念,那就是负数(Negative numbers)。负数的概念在小学数学里就有介绍,也就是说,小学生也应该能够自信地进行负数的各种运算,但是在公元18世纪以前,即使是当时欧洲的数学家,想让他理解“负数”这个概念也并不容易。“负数”在当时被认为是荒谬的,就像公元500年之前,毕达哥拉斯学派的弟子希伯索斯(Hippasus)发现无理数(也称为无限不循环小数,不能写作两个整数之比)一样,人们在直观感受遭遇挑战的时候往往先选择拒绝。
Hippasus
例如,当时的人们可以很直观地理解,如果你家有4条狗,后来送给别人家3条,你还剩下1条,4-3=1。但如果说你家有3条狗,然后送给别人家4条狗,那这是什么狗?!幽灵狗?
所以,1759年英国数学家Francis Maseres,也会说:“Negative numbers darken the very whole doctrines of the equations.(负数使关于方程的所有学说变得毫无意义,即认为负数没有意义)”。即使是欧拉(Euler),也为“负数”的概念纠结了好一阵,不过现如今,认为负数“无用”或“不合逻辑”才是真的荒谬。
那为什么人们对负数的理解发生了180°的大转变呢?因为我们发明了一种具有有用属性的理论上的数字,负数并不能很好地用来描述我们看得见、摸得着的可直观感受的事物,但却能很好地描述某种关系,例如债务。人们会在日常支出中记录各种交易信息,如果欠别人50元,你会记录-50,在赚了100元以后,可以直接用100+(-50)=50来计算属于自己的钱,而不需要更多的文字描述,负数已经将这种关系植入其中,既然有这种属性,又有什么理由说它是无用的呢?可见“关系”的重要性~
虚数也有相似的命运,从其名字就可以看出似乎受到过很不公正的待遇。我们能够得到方程x2 =1有两个解,x=1和x=-1。那对于方程x2 =-1呢?在解之前,我们不妨先假设x的解存在,就像负数一样,奇怪的概念往往其实有其自身的价值。
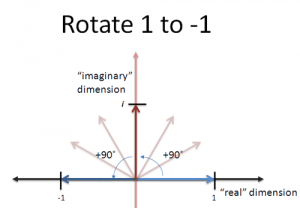
对于方程x2 =-1,其实可以写成1·x·x=-1。我们将x看成是一种“变换”,通过两次这种变换,我们最终将1变为-1。但我们不能通过两个正数的相乘抑或是两个负数的相乘来实现1到-1的转变。
但是如果这种“变换”是“旋转”呢?听起来很疯狂,但是我们把x定义为“逆时针旋转90°角”的话,在包含两个正交轴的坐标系上,就能够实现1到-1的转变。而这个坐标系构成的平面也称为“复平面(横轴为实数轴(Real Dimension),纵轴为虚数轴(Imaginary Dimension))”,并用字母i作为该情况下x的解来特指“逆时针旋转90°角”的变换。
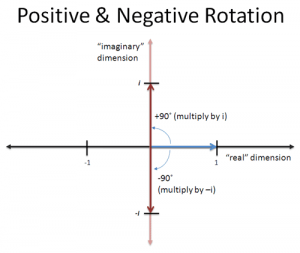
那如果想顺时针旋转90°呢?
答案是:乘以-i就行了。
而且如果乘以两次-i,和乘以两次i一样,得到的也是-1。
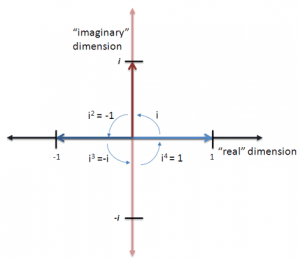
如果分别乘以0次、1次、2次、3次、4次、5次i,可以得到:
可以得到一下结论:
1=1(毫无疑问)
i=i(感觉是句废话)
i2=-1(上面已经说明了原因)
i3=(i·i)·i=-1·i=-i(三次旋转逆时针90°,相当于顺时针旋转90°,如上图)
i4=(i·i)·(i·i)=-1·-1=1(四次旋转逆时针90°,回到初始位置,一次循环结束)
i5= i4·i=i(开始下一循环)
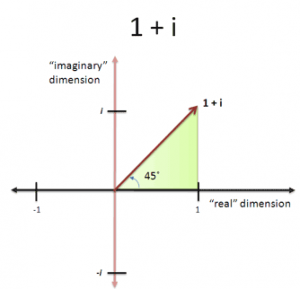
然而我们也不知不觉地将数从一维的实数拓展到了二维的复数,即实数与虚数的组合。或者说:复数=实部+i·虚部。例如,一个复数X的实部为1,虚部也为1,则可以得到复数X=1+i。复数X可以看作是复平面上的点(1,i),其在实轴与虚轴上的投影值即为实部与虚部的值,其长度或“模(Modulus)”为该点到原点的距离,该点与原点连线后与实轴正方向的夹角为45°,该角度称为幅角(Argument)。既然又有长度又有方向,因此复数也就可以看做是复平面上的一个矢量。
如果用Z代表一个复数,则可以写成更为普遍的形式:
z=a+bi
其中,a和b分别为复数Z的实部和虚部。
下面进行一个复数的实例计算,需要记住的一点是两个复数相乘就是让它们的模相乘得到最终的模长,让它们的幅角相加得到最终的幅角。
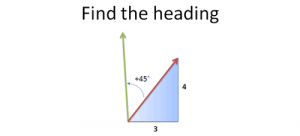
假设我们在一艘帆船上,现在帆船的航向是每向东前进3个单位就会向北前进4个单位,如果现在想改变航向,使其沿逆时针方向旋转45°,那新的航向是怎么样的?
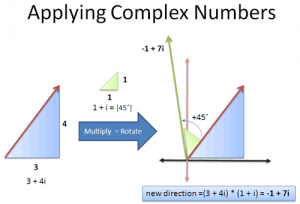
如果放在复平面上,船的位置在圆心处,那么当前的航向可以直接用复数表示,即3+4i。如果想逆时针转45°可以让该复数与1+i相乘,因为1+i的幅角正好等于45°。
画出图就很直观了,新的航向是每向西前进1个单位就会向北前进7个单位。
幅角为tan-1(7/-1)=98.13°。注意,如果要保持航速不变的话还需要在上面计算结果的基础上再除以根号2,因为复数1+i的模为根号2。
Reference

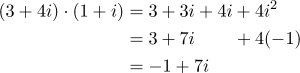
《虚数不“虚”》有1个想法